[딥러닝] Graph Neural Networks(GNN) 1 - Node embedding : background ~ random walk ~ deepwalk ~ node2vec
이 글에서는 기본적인 GNN에 대한 내용과 shallow encoder node embedding 방법인 random walk, Deep walk, node2vec, metapath2vec을 다루고려고 합니다.
image, text 등 graph와는 다른 data들에 대한 deep learning model들도 task에 관계없이 data에서 feature를 추출하는 것을 학습하는 것이 핵심입니다. GNN도 기본적으로 이들과 동일하게 graph 라는 data에서 feature를 학습하는 방법입니다. 학습된 모델로 입력 graph에서 뽑은 feature를 가지고 task에 맞게 사용하게 됩니다.
graph 에서의 ML task
- Node classification : node class 예측. node classification 은 transductive learning으로 일반적인 supervised learning 에 쓰이는 inductive learning과 차이가 있음.
- Link prediction : node 간 연결(연관)이 있는지 없는지 예측. 친구 추천이나 상품 추천에 활용
- Community detection : graph 나누기. 모여있는 node들을 clustering. retrieval 이나 data mining에 활용
- Network similarity : 두 network 비교
* inductive learning vs transductive learning ?
GNN 공부를 하게되면 transductive learning이 나오게 되는데, transductive learning은 test에 사용될 모든 data까지도 알고 있는 상태로( 전체가 labeling 되어있진 않으나 feature는 모두 알고 있는 상태) 학습하여 전체에 대한 답을 찾는 것으로 GNN은 보통 transdutive learning 상황이 많다. 보통 deep learning 하면 inductive learning 상황이 많다. GNN에서 inductive learning이라면 graph에 아예 없던 node들 즉 새로운 sub graph 가 학습된 graph에 추가되었을 때 이 sub graph의 feature를 어떻게 나타낼 것인가에 대한 문제로 볼 수 있다.
graph 는 왜 어려운가 ?
CNN은 입력 크기가 고정되어 있고 text, sequence도 embedding 하고 나면 일정한 입력 format으로 다룰 수 있으며, 순서가 정해져 있습니다.
graph는 크기도 다르고, 순서가 정해져있지 않아 어디가 시작인지 알 수 없습니다(node isomorphism problem) 또한 node에 다양한 type의 feature가 섞여 있을 수 있습니다.
graph 종류
GNN에서 다루게될 data인 graph에 종류는 아래와 같이 나뉩니다.

- homogeneous graph : social network ( undirected, unweighted homogeneous graph ) 보통 adjacency matrix로 표현
- heterogeneous graph : community-based QA sites, multimedia networks, knowledge graph ... type이 다른 edge를 표현하기 위해서 여러 adjacency matrix를 사용하기도 함.
- graph with auxiliary information : node들의 feature 정보가 주어지는 경우. 이 정보들을 어떻게 합치는지가 문제가 된다
- graph constructed from non-relational data : graph 형태가 아닌 데이터들도 graph 형태로 만들어서 접근 할 수 있음
GNN의 발전
GNN 은 shallow encoder를 써서 node embedding을 하는 random walk, Deep walk, node2vec, metapath2vec 으로 시작하여 DNN을 사용하여 graph를 표현하는 GCN, GAT, HAN, GTN 까지 발전되어 왔으며, 크게는 task dependent learning 이 가능한가 ? heterogeneous graph 처리가 가능한가 ? metapath를 알아서 찾아내는가 ? 로 구분될 수 있다.
이 글에서는 random walk, Deep walk, node2vec, metapath2vec 방법 (shallow encoder node embedding )까지만 다루고 있다
최근에 GCN2는 GNN 중 처음으로 DNN 이라 부를 수 있을 만큼 layer를 깊게 쌓는데 성공함. GCN2이전 GNN들은 over smoothing 문제로 인해 4 depth 이상 layer를 쌓지 못했다. ( GNN에서 layer 하나는 1 hoop이 되는데 보통의 graph들을 4 hoop이면 모두 연결됨 )
node embedding
GNN 은 node embedding에 대한 이해부터 시작합니다.

목표 : node를 d-dim으로 표현할 embedding 을 찾는 것. 이 때 비슷한 node 들(graph에서 관련이있는 node들)은 가깝도록 embedding 되어야 함.


graph setup : vertex set V와 Adjacency matrix A만 주어지고 node feature와 기타 정보는 없음
node embedding 학습을 위해 3가지를 정해야 한다
1. encoder 정의
2. node similarity function 정의
3. 아래 식에서 node similarity 를 정의하고 이에 맞게 encoder parameter 최적화. 아래 식에서 좌항 similarity(u, v)는 graph 상에서 u, v의 관계를 의미하고 우항은 node를 embedding한 vector 간 내적(cos similarity) 이다. 이 둘이 같아지도록 embedding 해야한다.

encoder 정의 : shallow encoding ( embedding lookup )
가장 간단한 encoder는 embedding lookup 방식이다. vertex(node) 수 만큼의 row를 갖는 embedding table(matrix) 가 있고, vertex index 가 raw index가 되서 해당 raw vector를 embedding vector로 쓰는 방식이다. shallow encoding 이라고도 부른다
node2vec, DeepWalk, LINE이 이러한 embedding table 을 학습하는 방법이다. 이후에 DNN 기반 encoder 가 나오기 전까지 쓰인 방법이다.
node similarity 는 어떻게 정의할까 ? ( loss function 정의 )
node 간 연결여부 ? 겹치는 neighbor 수 ? 비슷한 sub graph structural ?
아래 3가지가 node similarity로 쓰이는 방법들이다. 이 중 결국 random walk 방법이 쓰이고 있다.
- adjacency-based similarity : 아래와 같은 loss function 사용하며 모든 vertex 쌍에 대해 MSE 를 계산해야해서 vertex가 많아지면 계산량이 너무 커지는 단점이 있다. O(V^2). 계산량 문제 뿐 아니라 이 방법은 직접 연결되어 있는 node 관계(1 hoop) 에 대해서만 고려하고 있다. 2 hoop 이상 떨어진 node 들 사이의 관계는 embedding에 담지 못하는 큰 한계가 있다.
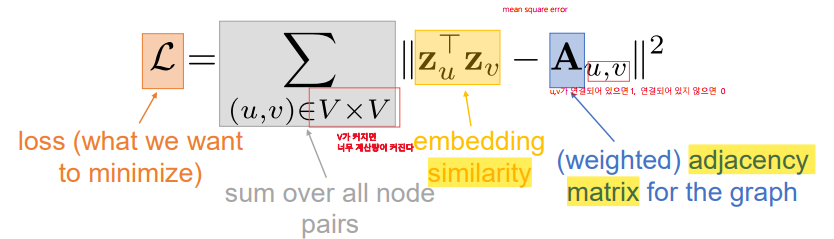
- multi-hop similarity : adjacency-based similarity가 multi-hoop 에 대해 담지 못하는 한계를 극복하기 위해 나온 방법으로 hoop 마다 adjacency matrix를 만든다. 4 hoop 까지 보려면 adjacency matrix는 4개가 있는 것이다. 그런데 이 A matrix들로 위의 loss function 처럼 단순히 연결되었나 안되었나만 고려하는 것으로는 graph 에서 node들간 관계를 나타낸다고 보기 어렵다. 이를 위해 단순 연결/비연결이 아니라 jacard similarity를 사용해서 두 node 사이 어느 정도 겹치는게 있는지를 식에 넣는다. ( S_u,v ). 하짐나 이 방법 역시 여전이 계산량이 O(V^2)으로 많으며, node similarity로 jaccard similarity를 쓰는 등 사람의 제어가 들어간다는 한계가 있다.
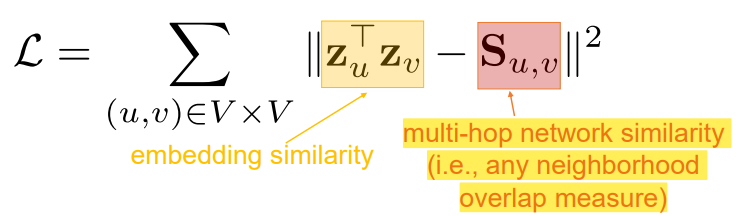
- random walk approaches : 위 두 방식의 한계를 보완하는 방법이다.
random walk
graph에서 node 간 관계를 random walk로 sequence하게 뽑고 이 확률로 embedding 하는 방식이다. 반복해서 random 하게 graph를 돌아다니며 sequence를 생성하므로 관계가 있는 node들은 같은 sequence(random walk)에 포함될 확률이 높아지므로 embedding도 가깝게 될 수 있다. random walk 수는 조정할 수 있으며 random walk를 모든 vertex에서 3번씩 시작되도록 하면 cost는 O(nV) 가 된다. 또한 graph가 확장되었을 때, 추가된 부분에 대해서 random walk를 하면 embedding이 가능해서 graph 확장에도 유연하다.
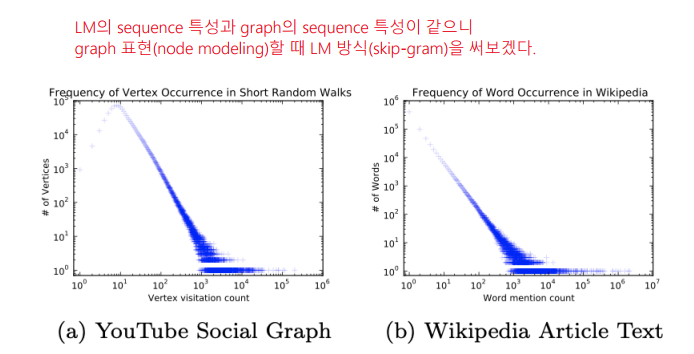
* random walk를 하다보면 power low 특징이 보이는데 이 특징들은 자연어에서도 나타나고 있다.
random walk loss function
아래 식을 최소화하는 z_u를 찾는 것이 optimization 이다.

하지만 이 식에서 모든 vertex에 대해서 exp(z_u @ z_n)을 해야하는 것이 cost가 크니, 모든 vertex에 대해 계산하지 않고 k 개의 negative samples 에 대해서만 위 식과 같이 계산하여 계산량을 줄이는 방법을 선택한다.

DeepWalk
: random walk 에서 뽑은 node sequence를 word2vec 과 같이 skip gram 으로 학습 하는 방법입니다. random walk 에서도 언급했듯이 random walk로 뽑은 node sequence는 자연어와 같이 power low 특징을 보이는데, 특징이 비슷하다면 자연어에서 word embedding 시 효과적이였던 skip gram으로 graph node embedding도 잘되지 않을까? 하는 아이디어 입니다.
random walk와 deep walk의 한계는 length가 고정되며, bias를 넣을 수 없다는 것 입니다. 이를 보완하기 위해 biased walk 인 node2vec이 제안되었습니다.
node2vec
graph 탐색시 BFS로 하면 local view를 파악할 수 있고, DFS로 global view를 파악할 수 있으니, 이 둘을 섞는다는 아이디어 이다.
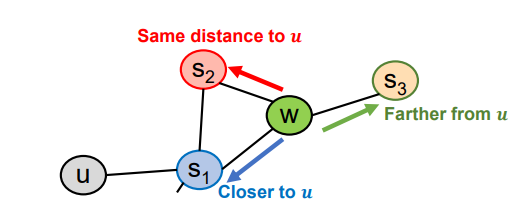
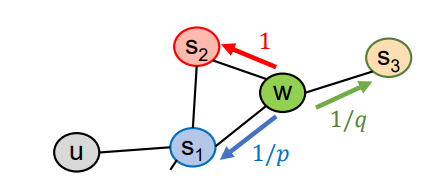
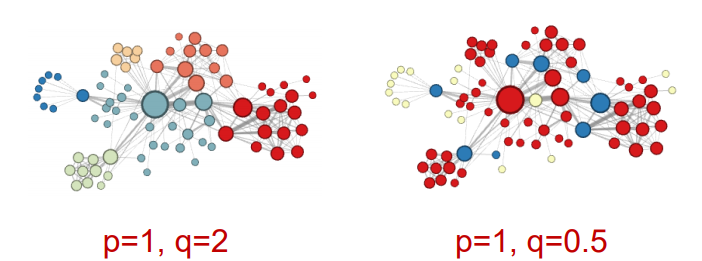
node2vec에서 p,q 를 조절함으로써 global view를 파악할지 local view를 파악할지에 대한 bias는 넣을 수 있었으나, 실제 graph(heterogeneous graph)에 존재하는 node 간의 관계(metapath) 까지는 넣지 못하는 한계가 있다.
그래서 graph에 미리 존재하는 node 간의 관계를 기반으로 node embedding 하는 metapath2vec 방법이 제안되었다.
metapath2vec
graph에 미리 존재하는 node간의 관계라는 것은 예를 들면, 사람들이 영화를 찾을 때 어떤 영화를 보고 그 영화의 감독이나 배우, 제작사를 찾아보고 이들과 연관된 영화들 중 하나를 다시 보게되는게 흔한 path이다. 이와 같이 영화 - 감독 - 영화, 영화- 배우- 영화, 영화-제작사-영화라던지, 논문-저자-논문, 논문-학회-논문과 같이 graph에 흔히 나타나는 node type간 관계를 metapath라 한다.
당연하게도 이 metapath를 미리 알고 있다면, node embedding 시 이 metapath에 따라 walking 하고 이를 토대로 학습하면 graph를 잘 표현할 수 있게 된다.
여기까지가 node embedding에 사용되는 shallow encoding에 대한 내용이다.
shallow encoding은 vertex 수 만큼의 embedding vector가 존재해야 한다는 cost와 처음나오는 vertex나 sequence에 대해서는 아예 파악하지 못하는 문제가 있다.
이러한 문제들을 보완하기 위해서 deep learning 기반 GNN이 등장하기 시작한다.
